1- Cálculo da distância real.
Exercício: Num mapa com a escala 1/100 000 duas localidades localizam-se a 4 cm de distância uma da outra. Calcula a distância a que estas duas localidades se encontram na realidade.
DADOS
Escala = 1/100 000
d. mapa= 4cm
D. real = X
RESOLUÇÃO
Mapa ------------------ Realidade
1 ---------------------------- 100 000
4cm ------------------------ X
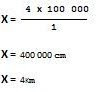
R: A distância real a que as duas localidades se encontram é de 4 Km.
Exercício: Num mapa com a escala 1/100 000 duas localidades localizam-se a 4 cm de distância uma da outra. Calcula a distância a que estas duas localidades se encontram na realidade.
DADOS
Escala = 1/100 000
d. mapa= 4cm
D. real = X
RESOLUÇÃO
Mapa ------------------ Realidade
1 ---------------------------- 100 000
4cm ------------------------ X
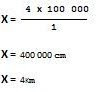
R: A distância real a que as duas localidades se encontram é de 4 Km.
2- Cálculo da distância no mapa.
Exercício:
Duas cidades localizam-se a 200Km de distância. Num mapa com a escala 1/10 000 000 qual a distância a que se encontram?
DADOS
Escala = 1/10 000 000
d. mapa= X
D. real = 200Km = 20000000cm
RESOLUÇÃO
Mapa ---------------------- Realidade
1 ---------------------------- 10 000 000
X ---------------------------- 20 000 000cm
R: A distância no mapa a que as duas localidades se encontram é de 2 cm.
3- Cálculo da escala.
Exercício:
Uma avenida está representada num mapa por um segmento de recta com 5 cm de comprimento. Sabendo que a avenida mede 500 metros de comprimento, calcula a escala do mapa.
Uma avenida está representada num mapa por um segmento de recta com 5 cm de comprimento. Sabendo que a avenida mede 500 metros de comprimento, calcula a escala do mapa.
DADOS
Escala = 1/X
d. mapa= 5 cm
D. real = 500m = 50000cm
RESOLUÇÃO
Mapa ---------------------- Realidade
1 ---------------------------- X
5cm ------------------------- 50000cm